GNavigia - Höhen glätten
Gedanken um ein schwieriges Thema
Ich schreibe praktisch keinen Code, den ich nicht selbst gebrauchen könnte. Vor über zwanzig Jahren hatte ich zusammen mit meiner damaligen Frau eine ausgesprochen spannende Radtour durch die französischen Alpen unternommen. Begleitet von den Aufzeichnungen im Tagebuch und meiner treuen Olympus OM-2 konnte ich viele Jahre später eine Geschichte darüber schreiben und weitere 10 Jahre später die Radtour auf der Grundlage von OSM Daten mittels GNavigia digitalisieren und dabei Höhen aus SRTM-Daten aus einer lokalen PostgreSQL-Datenbank interpolieren. Großartig. Aber: Die Höhen waren irgendwie seltsam. Und während der erste Tag über den Col d'Ornon und den ungleich aufregenderen Col de la Croix der Fer, den «Eisenkreuzpass», von la Mure nach St. Jean de Maurienne hinsichtlich der Tageskilometer auf 1% genau stimmte, hatte ich für den Col d'Ornon 800 Höhenmeter Steigung aus den großartigen Karten der Michelin 1:200000 Serie abgegriffen - und über 1650 aus den digitalisierten Daten berechnet.
Nachdem ich zahlreiche Skigebiete mittels GPS bis in die letzte Ecke hinein vermessen habe, ist mir klar, dass nicht die äußerst primitive Interpolation, beschrieben auf einer eigenen Seite, Schuld ist an den Differenzen, sondern die mangelnde Glättung der Daten. Wenn man nämlich die Höhenlinien der SRTM Daten und die OSM Kartendaten zusammen projiziert, erhält man in koupiertem Gelände eine um die Höhenlinie meandrierende Trassenführung, die ein ständiges Auf und Ab mit sich bringt. Dieses wiederum sorgt für die große Diskrepanz zwischen Wunsch und Wirklichkeit. In ebenem Gelände ist die Höhendifferenz übrigens fast zu vernachlässigen, eine Glättung nahezu überflüssig. Das gilt auch, wenn man die Abstände zwischen zwei digitalisierten Punkten groß hält, was den Charakter einer Passstraße aber eher ignoriert. Eine ähnlichen Effekt hatte ich mit den Messdaten der 4 Runden Rad am Ring 2010.
Damit ist klar, dass die Höhen geglätttet werden müssen, und zwar so, dass die Stützpunkte für die Lage nicht verloren gehen, Die Höhen müssen geeignet interpoliert werden. Alles, was ich hier erzähle, gilt für Höhen, die in geringen Abständen digitalisiert oder aufgezeichnet wurden. In der letzten Zeit hat sich, vermutlich durch das Marketing seitens Garmin und anderer Anbieter, eine unselige Gemeinde von Verfechtern der Theorie herausgebildet, dass die barometrische Höhenmessung eine großartige Sache sei.
Sie ist es - und sie ist es nicht! Die Höhe, die ein GPS-Empfänger mit SIRF-StarIII/IV oder MTK-3318 Hardware ermittelt, ist ungleich zuverlässiger als eine barometrische Höhenmessung. Der Luftdruck (und nichts anderes wird da gemessen), ist nicht genauer zu bestimmen als auf 10 Meter. Zudem kann er binnen weniger Stunden um bis zu 100 m schwanken. Ich habe, das habe ich schon auf anderen Seiten bekannt, meinen Garmin Vista HCx wieder verkauft, weil die barometrische Höhenmessung für all jene Zwecke völlig ungeeignet ist, wo der Empfänger freie Sicht auf Satelliten hat, insbesondere in baumlosen Skigebieten. Wenn sie darüber hinaus nicht abschaltbar ist und sich das Gerät nur beim Einschalten selbst synchronisiert, kommt das Gerät weg!
Funktionalität «Höhen glätten»
Die Funktionalität «Höhen glätten» erreicht man, sofern genau ein Track selektiert ist, aus dem Menü via Bearbeiten/Track/Höhen glätten. Es existiert ein Shortcut für diese Aktion. Vor dem Start erscheint ein Dialog, der Art und Parameter der Glättung abfragt. Die Höhen des Tracks sind am Ende der Berechnung mit den neuen Werten überschrieben. Vor der Anwendung einer anderen Funktion muss daher die Aktion rückgängig gemacht werden (Strg+Z). Sonst arbeitet die nächste Funktion auf den bereits geglätteten Höhen.
Funktionalität «Ursprüngliche Höhen»
GNavigia speichert die originalen, ursprünglichen Höhen («genuine heights»). Darunter versteht das Programm die allererste Höhe, die für einen Trackpunkt gesetzt wird. Wenn Sie bei der Glättung der Höhen angeben, dass die ursprünglichen Höhen benutzt werden sollen, wird auf diesen gearbeitet. Dadurch können Sie die Glättung mehrfach aufrufen, ohne die zuvor durchgeführte rückgängig machen zu müssen oder auf bereits berechneten Werten aufzusetzen. Außerdem können Sie nun in aller Ruhe darauf warten, dass Ihnen GNavigia eines Tages eine bessere Methode zur Glättung anbietet. Die originalen Daten bleiben prinzipiell auf immer erhalten. Um diese Werte, die ja grob falsch sein könnten, zu ändern, müssen Sie aber nicht von Hand in die GTD-Datei eingreifen. Vielmehr können Sie über den Menüpunkt Bearbeiten/Trackpunkt/Korrigiere ursprüngliche Höhe Änderungen vornehmen. Sinngemäß gilt das auch für Wegpunkte.
Über den Menüpunkt Bearbeiten/Track/Ursprüngliche Höhen wiederherstellen wird
ein Track oder eine Liste von Tracks hinsichtlich der Höhen wieder in den Ausgangszustand
versetzt. Sind mehrere Tracks selektiert, erfolgt zuvor eine Sicherheitsabfrage.
Allerdings sollten Sie beachten: Wenn Sie in älteren Versionen Höhen interpoliert oder
von Hand geändert haben, werden diese Höhen beim Einlesen in der neuen Version als
ursprüngliche Höhen gespeichert. Die Messwerte vor dieser Änderung bringt Ihnen niemand
wieder zurück.
Methoden der Glättung
Sowohl beobachtete als auch aufgezeichnete Höhen sind mit systematischen Fehlern behaftet und stellen keine normalverteilten Beobachtungen im Sinne der Statistik dar. Daher gibt es für die Glättung von Höhen auch nur sehr unbefriedigende Modelle. Andererseits ist die Frage natürlich erlaubt, was man mit der Glättung erreichen will. Und das entscheidet man doch am Besten im «Angesicht der Reiseroute». Die Frage der Glättung von Höhen ist ja auch immer die, wieviel man am Ende verschwinden lassen möchte.
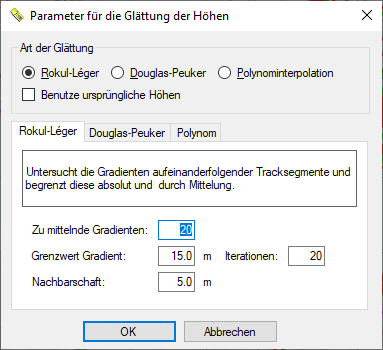
GNavigia benutzte zur Glättung der Höhen bevorzugt die von Rokul und Léger angegebene, stufenweise und iterativ vorgehende Methode. Anders als die Methode nach Douglas-Peuker bleiben die Extremwerte dabei nicht erhalten. Sie ist dazu geeignet, grobe Fehler zu eliminieren. Ohne allzu intensiv auf die mathematischen Grundlagen einzugehen, sei kurz erläutert, dass die Methode aus 4 Schritten besteht:
- Local Smoothing (lokale Glättung) zur Begrenzung des Gradienten auf einen festen Maximalwert. Im Parameterdialog wird dieser in den Feldern Grenzwert Gradient und Iterationen abgelegt.
- Mittelung der verbesserten Gradienten. Diese erfasst nicht nur die im Feld Zu mittelnde Gradienten angegebene Anzahl an Gradienten, sondern nutzt für die zweite und alle nachfolgenden Berechnungen die Hälfte der zuvor gemittelten Gradienten, sodass der Übergang zwischen den Abschnitten eher sanft verläuft.
- Lokale lineare Interpolation, dieser Durchgang interpoliert iterativ verbleibende Gradienten, die den Grenzwert übersteigen. Außerdem werden alle Punkte erfasst, die einen alternierenden Gradienten aufweisen. Dieser Schritt ist in besonderem Maße werterhaltend und glättend zugleich.
- Berücksichtigung der Nachbarschaftsverhältnisse. Die in angegebener Nähe liegenden Punkte werden in der Höhe gemittelt.
Die 590 Punkte des Col d'Ornon werden auch auf älteren Rechnern trotz der vielen
Rechenschritte sehr schnell berechnet. Mit dem Verfahren nach Rokul-Léger,
hier mit den Standardparametern angewendet, werden auch neuralgische Abschnitte
(Serpentinen) gemeistert und sauber geglättet. Der Wert TotalUphill zeigt
907 Meter, was mit den aus der Karte ermittelten Daten schon recht gut übereinstimmt.
Zudem werden in kleinmaßstäbigen Karten nur die Extremwerte eingetragen und nicht
kleinere Zwischenanstiege.
Die Methode nach Douglas-Peuker mit einem Grenzwert von 50 m. Die Glättung wirkt unnatürlich stark, kleinere Grenzwerte führen aber u. U. zu Gegenanstiegen, die auf zu große Ausreißer in den Höhendaten hindeuten. Extremwerte bleiben erhalten, ganz gleich ob richtig oder falsch.
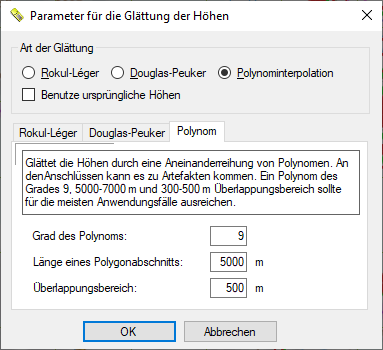
Die Glättung durch Polynominterpolation ist ebenso aufwändig zu programmieren wie leicht falsch zu gebrauchen. Wer diese Form der Glättung wählt, sollte wissen, was er tut. Mathematisch wird ein Modell nach der Methode der kleinsten Quadrate verwendet, das wie folgt aufgestellt wird:
yi = a0 + a1xi1 + a2xi2 + a3xi3 + ... + anxin ,
darin ist xi die Strecke vom Anfang des Tracks (respektive vom Anfang des Teilabschnitts) und yi die Höhe in diesem Punkt. Der größte Exponent (n) bestimmt den Grad des Polynoms. Aufgrund der extrem schnell steigenden Zahlenwerte ist das Polynom auf Grad 11 begrenzt.
Wegen der großen Anzahl der Höhenwerte und der geringen Anzahl
an Unbekannten (Grad des Polynoms + 1) handelt es sich zwar formal um ein Ausgleichungsproblem
mit sehr vielen Überbestimmungen, die «Beobachtungen», also die Höhen, sind allerdings nicht
normalverteilt. Obgleich hier der Cholesky-Algorithmus zur Anwendung kommt, der auch schwierige
Normalgleichungssysteme ohne Pivot-Suche numerisch stabil invertieren kann, ufern die Potenzen
zum Teil gewaltig aus. Es ist daher nicht ratsam, diese Berechnungen für lange Distanzen
durchzuführen, ohne zuvor eine Sicherungskopie der Daten zu machen! Hier kann selbst das
Undo versagen.
Die Polynominterpolation sollte niemals auf den gesamten Track angewendet werden, sondern immer nur auf einen Teil davon. Sie können zwar astronomische Werte unter Länge des Polygonabschnitts eingeben, aber Sie sollten es hier bei maximal 10 km belassen. Ist der angegebene Wert größer als die Tracklänge, wird der ganze Track berechnet. Standard ist 5 km. Ein ungerader Polynomgrad hat sich als sinnvoll erwiesen, da er Steigungswechsel besser beschreibt. Der Überlappungsbereich kann höher gesetzt werden, es werden aber nicht die geglätteten Werte der Berechnung zuvor genommen, sondern die Rohdaten. Dennoch wirkt das Ergebnis auf den ersten Blick stetig; dass die erste Ableitung nicht mehr stetig ist, erkennt man spätestens am Höhendifferenzprofil. Restbereiche werden verteilt. Die Länge des Polygonabschnitts ist also meist etwas größer als angegeben, im Beispiel sind es tatsächlich 10700 m. Zu den Bereichen 2-4 kommt noch der Überlappungsbereich hinzu, sodass diese de facto 11 km lang sind. Für die 22 Kilometer der Nürburgring-Nordschleife würde man etwas kleinere Abschnitte wählen.
Die Polynominterpolation liefert deutlich gefälligere Werte als die Glättung nach Douglas-Peuker. Mir persönlich gefällt das Ergebnis für 9-10000-1000 noch besser als das hier dargestellte, aber für jedes Gelände ergibt sich eine bestmögliche Kombination von Werten.
Weitere Methoden sind angedacht, aber nicht in Vorbereitung.
